Promotion purchase condition model
This topic discusses how to define and evaluate a single promotion. In particular, it discusses how to define the purchase conditions of a promotion.
Conceptually, a promotion has conditions and rewards. When the conditions of the promotion are satisfied, the corresponding rewards are calculated and applied to an order. A promotion has many types of conditions associated with it.
Primarily, there are 5 different types:
- Schedule conditions that limit the promotion such that it is applicable only within a certain period of time.
- Targeting conditions that restrict the application of a promotion to a subset of customers.
- A Promotion code condition which requires that a correct code to be entered before the promotion can be applied.
- An application limit constraint which limits the number of times a promotion can be applied either to an order, to a customer, or overall.
- A Purchase condition which requires the customer to have purchased a certain combination of products, or spent a certain amount on a certain combination of products.
When all of the conditions are satisfied, the rewards are calculated and applied.
The first four types can be considered pre-conditions. They are the constraints a customer must satisfy before the purchase condition is even evaluated. They generally have a simple model and are easy to implement. This document focuses on how to properly model the last type of condition: the purchase condition, and how to calculate rewards in a promotion. It uses mathematical expressions to describe a purchase condition in a promotion and the associated rewards. It also defines the algorithm to evaluate a purchase condition and to calculate the associated rewards.
Observations
These are based on some typical promotions, defined below. While these promotions may not be applicable to your store, they represent common patterns:
- Buy one to three bottles of water and get 10% off, buy four to six bottles and get 20% off, buy seven or more and get 30%.
- Get 10% off the first three bottles of water, 20% off the next three, and 30% of any additional water bottles purchased.
- Buy three bottles of water for $20.
- Buy a water cooler and one bottle of water for $129.
- Buy a water cooler, and then buy up to four bottles of water at 50% off.
- Buy three three-gallon or five-gallon water bottles and get 10% off.
- Buy three water bottles of the same size (either three-gallon or five- gallon), and get 10% off.
- Buy a water cooler and a five gallon water bottle, and get 10% off the water cooler and get the water bottle for $1.
- Buy a water cooler and a water bottle for $129 or free shipping.
- Buy a water cooler and a water bottle for $129 and free shipping.
- Buy a water cooler and a water bottle valued at $150 or more, and get free shipping.
- Spend $100-$200 on water bottles, and get 10% off; $200 to $300, and get 20%; spend $300, and get 30% off.
First, determine how to determine whether a promotion is applicable. Consider promotions 1 and 2:
- Buy one to three bottles of water and get 10% off, buy four to six bottles and get 20% off, buy seven or more and get 30%.
- Get 10% off the first three bottles of water, 20% off the next three, and 30% of any additional water bottles purchased.
This is usually what a cashier would do at the check-out counter:
- Find all water bottles in an order.
- Based on the quantity determine which range the quantity falls in.
- Applied the adjustments associated with that range to the water bottles.
A more abstract description of the preceding process:
- Identify purchase patterns targeted by promotion (one single water bottle is a purchase pattern targeted by the promotion; this pattern may occur multiple times in an order).
- Based on the number of times a pattern occurs, determine the distribution (one-three, four-six, or seven or more).
- Based on the distribution, calculate the rewards associated with that range (10%, 20%, or 30%).
Observation 1: The evaluation of a promotion may be done through a three-step process of pattern recognition, quantity distribution, and reward calculation.
This three-step process is used to determine whether a promotion is applicable.
Observation 2: A purchase pattern is usually defined by specifying some selection criteria, such as "any water bottle".
The difference between the two promotions lies in the way that the quantity distribution is handled. If you buy X number of water bottles, depending on where X falls, in promotion 1, each of the water bottles is discounted the same way, whereas in promotion 2, they will be divided into tiers and discounted differently. We call the first type of distribution a volume based distribution, and the second type, a tiered distribution.
Observation 3: The quantity distribution is either volume based or tiered.
In the previous samples, the purchase pattern is made up of one single item, that is, a bottle of water. This may not be the case. For example, in promotion 3: "Buy three bottles of water for $20", each unit of three bottles of water is the targeted purchase pattern.
Observation 4: There is usually a quantity requirement associated with the selection criteria. If a match of a purchase pattern is to be present in an order, both the selection criteria and the quantity requirement need to be satisfied.
In promotions 1-3, the promotion always targets a single type of item in the patterns, namely, a water bottle. In promotion 4: "Buy a water cooler and one bottle of water for $129", the targeted pattern is a combination of a water cooler and a water bottle. This leads to the next observation.
Observation 5: If each combination of a selection criteria and a quantity requirement is considered as a single constraint of a purchase pattern, a purchase pattern may be defined through multiple such constraints.
Consider promotion 5: "Buy a water cooler, take up to four bottles of water at 50%". In this case, if a customer buys one water cooler and one bottle of water, the purchase pattern is a match. If a customer buys one water cooler and two bottles of water, the purchase pattern is also a match; in fact if the customer buys one water cooler and anywhere between one and four bottles of water, the pattern is always a match.
Observation 6: The quantity requirement contained in the definition of a purchase pattern can be either a single value or a range.
Promotions 6 and 7 are defined as:
- Buy three three-gallon or five-gallon water bottles, get 10% off.
- Buy three water bottles of the same size, either three-gallon or five-gallon, get 10% off.
While both promotions target three and five-gallon water bottles, and the quantity requirement is the same (three), promotion 7 requires that all of the water bottles must be of the same size (homogeneous), promotion 6 does not (heterogeneous). Two three-gallon water bottles and one five-gallon water bottle would have satisfied promotion 6, but not promotion 7. Another way to look at this difference is to distinguish these two by the level at which the selection criteria are joined by a logical "or". In promotion 6, the "or" is at a lower level: three (three or five) gallon water bottles, while in promotion 7, the "or" is at a higher level: three three-gallon or three five-gallon water bottles.
Observation 7: When the selection criteria conveys a logical "or" semantic, and the quantity requirement indicates that a list is expected, the list may be either homogeneous or heterogeneous.
Promotion 8, "Buy a water cooler and a five-gallon water bottle, and get 10% off the water cooler and get the water bottle for $1", reveals that the targeted purchase pattern is a water cooler and a water bottle, while the rewards are different for the water cooler and the water bottle.
Observation 8: Rewards to different items in a target purchase pattern can be different.
Promotion 9, "Buy a water cooler and a water bottle for $129 or free shipping", presents a choice of either free shipping or a fixed price for the item.
Observation 9: Rewards for a purchase pattern can be presented as a choice of multiple options.
In promotion 10, "Buy a water cooler and a water bottle for $129 and free shipping", if the customer has purchased both a water cooler and a bottle of water, they get the package for $129 and the free shipping.
Observation 10: Multiple rewards can be applied to items in a purchase pattern.
Assume a customer has purchased two water coolers and two water bottles. One water cooler is an entry version priced at $69, and a water bottle priced at $10; the second is a deluxe water cooler priced at $169, and a water bottle priced at $20. If we apply promotion 11, "Buy a water cooler and a water bottle valued at $150 dollar or more get free shipping", to this order, two patterns of "1 cooler and 1 bottle" are identified. However, only the deluxe cooler and water bottle is eligible for the promotion.
Observation 11: A filter on matched purchase patterns is required in the some cases to narrow the matched purchase patterns to the ones targeted by a promotion.
Compare promotion 1 and 12:
- Buy 1 to 3 bottles of water get 10% off, 4 to 6 bottles get 20% off, 7 or more get 30%;
- Spend between $100-$200 on water bottles get 10% off; $200 to $300 get 20%; spend $300 get 30% off;
Notice that they target the same pattern: a water bottle. Both promotions have three ranges and the same reward associated with each range. The difference is that in promotion 1, a range is defined based on the number of water bottles purchased, while in promotion 12, the range is defined based on spending thresholds. This leads to our last observation:
Observation 12: The quantity distribution as mentioned in the three-step promotion evaluation process could exceed the distribution of quantity, it could be based on either quantity (or to be more precise, the number of matches for a purchase pattern in the order) or spending. Similarly, a spending threshold distribution can be volume based or tiered.
Henceforth, the generic term, "distribution" refers to both a quantity distribution and a spending distribution.
The model
First, let's list all of the observations made in the previous section:
- The evaluation of promotion may be done through a three-step process of pattern recognition, quantity distribution and reward calculation.
- Purchase pattern usually is defined by specifying some selection criteria (any water bottle).
- The quantity distribution could be a volume based or tiered.
- Besides selection criteria, there usually is a quantity requirement associated with the selection criteria. If a match of a purchase pattern is to be present in an order, both the selection criteria and the quantity requirement need to be satisfied.
- If each selection criteria and quantity requirement combination could be called one constraint of a purchase pattern, a purchase pattern may be defined through multiple of these constraints.
- The quantity requirement that is part of the definition of a purchase pattern can be either a single value or a range.
- When the selection criteria convey an "or" semantic and the quantity requirement indicates a list is expected, in some cases the list is a homogeneous list, in other cases the list is a heterogeneous list.
- Rewards to different items in a target purchase pattern can be different.
- Rewards for a purchase pattern can be presented as a choice of multiple options.
- Multiple rewards can be applied to items in a purchase pattern.
- A filter on matched purchase patterns is needed in the some cases to narrow the matched purchase patterns to the ones targeted by a promotion.
- The quantity distribution as mentioned in the three-step promotion evaluation process could be more than the distribution of quantity, it can base on either quantity (or to be more precise, the number of matches for a purchase pattern in the order) or spending, similarly a spending threshold distribution can be volume based or tiered.
Based on these observations, you can define the model for promotion using mathematical expressions.
These mathematical expressions require some common notations:
- A set is denoted using a pair of curly braces, "{}".
- A vector, or matrix, is denoted using a pair of brackets, "()".
- In a mathematical expression, a pair of brackets, "()", also conveys the priority of the operator association, for example, a*(b+c) means that the "+" takes priority over "*".
- In Sxi=x1+x2+...+xn, the semantics of the "+" operation varies based on operand types.
- []f is a floor operation to convert real numbers to integers.
- A range of number a to b are denoted by [a,b],[a,b),(a,b] or (a,b), a square bracket indicates the boundary is included in the range.
- < > denotes a tuple.
- F(X, Y, Z) denotes that F is a function of X, Y and Z.
- s is a SKU, which uniquely identifies a purchasable catalog entry.
- q is a quantity, it is a non-negative number.
- u is a unit cost, it is a non-negative number, for any purchasable catalog entries, when the SKUs are the same, the unit costs are always the same.
- l is a tuple consists of s, q, and u, <s, q, u>, called a line item.
- L is a line item set, that is, L={l1, l2, ... ln} such that !i,j where 0 < i<j < n+1, and li.s=lj.s. Note that L is not a vector, L is a scalar. Its type is a set.
- For l, the following comparisons are defined:
- li = lj when and only when li..s = lj.s and li..q = lj.q
- li lj when and only when li..s = lj.s and li..q lj.q
- lilj when and only when li..s = lj.s and li..q lj.q
- l= li-lj is valid when and only when li.s = lj.s, the result l is defined as l.s = li.s=lj.s and l.q =max{0, li.q-lj.q}
- l= li+lj is valid when and only when li.s = lj.s, the result l is defined as l.s=li.s and l.q = li.q+lj.q
- when L= {l1, l2, ... ln} the following comparisons are defined:
- ={};
- lic L, 1 i n;
- quantity(L) =;
- cost(L) =
- Li` Lj when lc Li, l'c Lj, such that l l'
- Li = Lj when Li` Lj and Lj` Li;
- Li4 Lj = Li + Lj is defined as:
L initially is set the same as Li, for each l in Lj, if l' in L such that l.s = l'.s, then l'=l'+l, otherwise, l is added to L, L=Li+Lj; - L=Li - Lj is defined as:
Initially L=
,
for each l in Li,{
if l' in Lj such l.s = l'.s {
l' in Lj such l.s = l'.s {
if (l.q>l'.q) {
l.q=l.q - l'.q;
add l to L; }else{ continue to next l; } } else { add l to L; } } - Li3 Lj is defined as L= Li3 Lj=Li- (Li-Lj)=Lj-(Lj-Li);
- first(L,x) is defined as the following:
initially, L' is empty,
starting from the first l in L, for each l in L while (x > 0) {
if l.q x {
L' = L'+{ l}; } else {l.q = x
L' = L'+{ l} - ;
} x=x-l.q }L' is first (L,x)
- group(L,z,x), where L is a line item set, z is the size of a group, and x is the index of that group. The function is defined as the following:
first(L,z*x)-first(L,z*(x-1))
- f is a filter (or selection criteria, refer to Observation 2), which is a function of L, that returns another L' such that L'=f(L) ' L, f can be defined by continuously applying a sequence of f's, that is f=f1(f2(...fn-1 (fn ())...)), that is, join a list of selection criteria using a logical "and".
 is a special type of filter where,
is a special type of filter where,  L,
L, (L)=
(L)= , fc is another special type of filter where
, fc is another special type of filter where  L, fc(L)=L;
L, fc(L)=L;
- F is a filter list, that is, a vector of filters (f1, f2, ..., fn);
- r is a weighted range of [m, n] where m and n are positive numbers m
 n, n is optional, when n is absent,
n, n is optional, when n is absent,  is assumed, w is the weight of r, 0w1. A weighted ranged is introduced to define the quantity requirement of a pattern definition. Refer to Observations 4 and 6.
is assumed, w is the weight of r, 0w1. A weighted ranged is introduced to define the quantity requirement of a pattern definition. Refer to Observations 4 and 6.
operations defined for r are: size(q,r) =min {max{m,q},(m*(1-w) + n*w)}L'=r*L is defined as:
if L={l1, l2,..., ln,} then r*L = L' = {l'1, l'2, ..., l'm} where
when i<m, l'i=li
l'm.q=[quantity(L)/size(quantity(L),r)]f*size(quantity(L),r) -;
l'm.s = lm.s;
m is determined by the following rules:
- mn
- [quantity(L)/size(quantity(L),r)]*size(quantity(L),r) -> 0
- [quantity(L)/size(quantity(L),r)]*size(quantity(L),r) -0
- R is a range list, that is, a vector of weighted ranges (r1, r2, ..., rn)
- A Pattern can be described as a collection of constraints, all of which must be satisfied. Refer to Observation 5. Each constraint defines that the number of SKUs that satisfy a selection criteria (f) present in the line item set (L) must fall within a certain range (r). Function Occ(L) calculates how many times a pattern occurs in the L and function P(L) finds all of the line items in L, then groups them into line item sets, each representing a match of that pattern;
For a given L, R=(r1, r2, ..., rn), and F=(f1, f2, ..., fn) and i,j, igj, fi(L)3 fj(L)=
:

P(L)={p1, p2, ..., pOcc(L)} where each pi is a line item set, it contains the line items that represent one match of the pattern. pi= ,
at(P(L),i)=pi is a function that returns the i-th match of the pattern. In the preceding formulas, R and F can be viewed as the configuration of the function, L is the parameter.
Expand the preceding concepts a bit further: if Mf =
mi and mj may not be equal and for any a, b, c, and d, |a-b|+|c-d|g0, 1a,bn,1cma, 1d mb fac(L)3 fbd(L)=
, then following are the definitions for Occ(L) and P(L) for given R and M, let , and F'=(f1, f2, ..., fn) then Occ(L) for R and M becomes Occ(L) for R and F', similar results can be derived for P(L).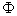
This construct is introduced to address the homogeneous list requirements mentioned in Observation 7. - For a pattern P(L)={p1, p2, ..., pOcc(L)} a pattern filter f is a filter, such that f(P(L))={pk1, pk2, ... pkm} and kic[1,Occ(L)] for any igj, i,jc[1,m] kig kj
Occ(f(P(L)))=m
at(f(L),i)=pki
The pattern filter concept is first mentioned in Observation 11.
- D is a distribution. D is a function of L, based on a pattern function P a pattern filter fp, and a segmentlist g= where 0 < minimaxi < mini+1, maxn is optional, when maxn is absent, maxn= is assumed. min and max can be the number of patterns present, or the spending threshold on patterns. L, P, fp and g can be viewed as the configurations of D. L is the parameter. There are two kinds of D, Dv and Dt, that is, a volume based range and a tiered range. Refer to Observation 3. For the quantity based distribution, Dv and Dtare defined below:
Let P'=fp(P(L))=fp({p1, p2,..., pk})={p'1, p'2,... p'm}


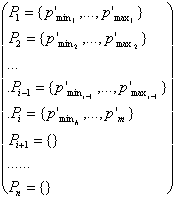
where minim maxi
Similarly, Dv and Dt can be calculated for the spending threshold based on the cost function of line item set. Refer to Observation 12.
- A purchase condition, can be described as the following:
A purchase condition works on an input parameter: line item set L, usually initialized based on the content of an order. It is defined by a distributionD. The distribution is configured by a pattern P, a pattern filter fp and a segment list g. The pattern functionP is configured by a filter listF and a weighted range listR.
If D(L)=, each pij is a line item set. It contains the line items in L that make up one match for the pattern; the content of Pi is determined by the distribution logic mentioned earlier in this document.
If for D(L)=(P1, P2,..., Pn)T and P1=P2=...= Pn={}, then the purchase condition is not satisfied, otherwise the purchase condition is satisfied.
- d is an adjustment function of line item set L. d is from a predefined set which includes but is not limited to elements of the following matrix. The elements in the matrix need to be configured before used to construct promotions, that is, the adjustment amount need to be set for FixedAmountOff:

- a is a reward function of a line item set L. L usually is a match of a purchase pattern, that is, it contains all of the line items that comprise a match for a purchase pattern. a is defined as: a (L) where:
For given (d1, d2, ..., dn) and (f1, f2,..., fn):
a(L)
In the preceding formula, d1, d2, ...,and dn as well as f1, f2, ..., fn can be viewed as the configuration of a and line item set L is the only parameter. The expression can be interpreted as the collective result of applying adjustment of di to a sub set of L as identified by filter fi.
the preceding definition reflects observation 8, where different items in the purchase pattern match can be rewarded differently. The filters fi determines the set of items in a purchase pattern match (L) that will be rewarded by applying di. to them.
Also, note that we did not specify that fi(L) 3 fj(L) has to be a empty set. When fi(L) 3 fj(L) is not empty, which means that certain items in L are rewarded by both di and dj, that is, multiple rewards can be applied to the same items. Refer to Observation 10.
- Once a purchase condition is satisfied, the three-step process of evaluating a promotion can be expressed as (a1, a2, ..., an)*D(fp(P(L))=(a1, a2, ..., an)*(P1, P2, ..., Pn)T . Refer to Observation 1:
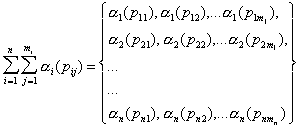
the result is a set, not a matrix. It is expressed in a line by line format to illustrate that each line has a different reward associated with it.
If a choice of different rewards can be granted for patterns in a segment in the distributions (Refer to Observation 9), the reward can be rewritten as:

Where 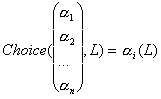
Examples
This section examines how to apply the preceding model to two real promotion examples:
Promotion 1: Buy between one and ten T-Shirts, and get 10% off the price, buy between eleven and one thousand, and get 20% off, buy more than one thousand, and get 30% off. This is an example of volume-based pricing.
Define the Promotion: Let
- Filters
- fc(L)=L (that is, fc does not eliminate any line items in L)
ft-shirt(L) = L' where i lic L' li belongs to category T-Shirt, F=(ft-shirt) - Pattern filter
- fpc(P(L))=P(L), it does not eliminate any patterns
- Weighted range
- r1=[1,1] with weight w=0 , R=(r1)
- Pattern is defined as
- P is configured by R, F, that is, (r1) and (ft-shirt)
- Distribution
- D =
and D is a volume based quantity distribution.
- Adjustment functions
- d1(L)= 10% off every item in L,
d2(L)= 20% off every item in L,
d3(L)= 30% off every item in L, - Rewards
- a1(L)=d 1(fc(L)),
a2(L)=d 2(fc(L)),
a3(L)=d 3(fc(L))
Apply the Promotion
- Scenario:
- Shopping cart contains:
- 10 Red XL T-Shirts
- 5 Red Green M T-Shirts
- 4 White M T-Shirts
- 10 pairs of sneakers
- Flow:
-
- Initialize:
L={l1,l2,l3,l4},
l1.s=RED XL T-Shirt, l1.q=10, l1.u=$10.00
l2.s=RED M T-Shirt, l1.q=5, l1.u=$8.00
l3.s=White M T-Shirt, l1.q=4, l1.u=$8.00
l4.s=Sneakers, l1.q=10, l1.u=$80.00 - Based on the preceding definition,
=19 P(L)={p1, p2,..., p19} p1= {l}, where l.s=RED XL T-Shirt, l.q=1, l.u=$10.00 .... p10={l}, where l.s=RED XL T-Shirt, l.q=1, l.u=$10.00 p11={l}, where l.s=RED M T-Shirt, l.q=1, l.u=$8.00 ... p15={l}, where l.s=RED M T-Shirt, l.q=1, l.u=$8.00 p16={l}, where l.s=White M T-Shirt, l.q=1, l.u=$8.00 ... p19={l}, where l.s=White XL T-Shirt, l.q=1, l.u=$8.00
- Initialize:
Next, perform filtering on the resulted pattern, distribute the result to the distribution defined above, and apply the rewards. The steps can be expressed as:
(a1,a2,a3)*D(fpc(P(L))) =(a1,a2,a3)*
The result of the preceding expression is: 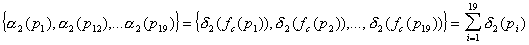
Promotion 2: Buy two or more of this list of products:"T-Shirts, Pens, or Glasses" for 20% off, and get free shipping for Club members.
When this promotion is created, the targeting condition is set to target Club members. Then, the definition of this promotion is reduced to:
Buy 2 or more of this list of products: "T-Shirts, Pens, or Glasses" for 20% off, and get free shipping:
Define the Promotion: Let
- Filters
- fc(L)=L (that is fc does not eliminate any line items in L),
ftpg(L) = L' where i lic L' li belongs to category T-Shirt, Pens, or Glasses, F=(ftpg) - Pattern filter
- fpc(P(L))=P(L), fpc is a pattern based filter, and it does not eliminate any patterns
- Weighted range
- r1=[1,1] with weight w=0 , R=(r1)
- Pattern is defined as:
- P is configured by R, F, that is, (r1) and (ftpg)
- Distribution
- D = ([2,
 )) and D is a volume based quantity distribution.
)) and D is a volume based quantity distribution. - Adjustment functions
- d11(L)= 20% off every item in L,
d12(L)= free shipping for every item in L, - Rewards
- a1(L)=(d 11, d12 )*(fc(L), fc(L))T= d 11(fc(L))+d 12(fc(L))
Apply the Promotion
Scenario 1:
Shopping cart contains:
- 1 Red XL T-Shirt
Flow:
1. Initialize
L={l1},
l1.s=RED XL T-Shirt, l1.q=1, l1.u=$10.00
2. Based on the preceding definition,
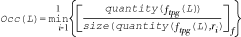
P(L)={p1}={{l}}, where l.s=RED XL T-Shirt, l.q=1, l.u=$10.00
Next, perform filtering on the resulting pattern, distribute the result to the distribution. The steps can be expressed as: D(fpc(P(L))) =({}), that is, the purchase condition is not satisfied.
Scenario 2:
Shopping cart contains:
- 1 Red XL T-Shirt
- 2 Wine glasses
- 1 Fountain Pen
Flow:
1. Initialize
L={l1,l2,l3 },
l1.s=RED XL T-Shirt, l1.q=1, l1.u=$10.00
l1.s=Wine glasses, l1.q=2, l1.u=$32.00
l1.s=Fountain Pen, l1.q=1, l1.u=$20.00
2. Based on the preceding definition,
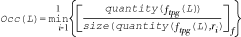
P(L)={p1, p2, p3, p4} p1= {l}, where l.s=RED XL T-Shirt, l.q=1, l.u=$10.00 p2={l}, where l.s=Wine glass, l.q=1, l.u=$32.00 p3={l}, where l.s=Wine glass, l.q=1, l.u=$32.00 p4={l}, where l.s=Fountain Pen, l.q=1, l.u=$20.00
Next, perform filtering on the resulting pattern, distribute the result to the distribution defined above and apply the rewards. The steps can be expressed as: (a1)*D(fpc(P(L))) =(a1)*(fpc({p1, p2, p3, p4}) = (a1)*({p1, p2, p3, p4}) = {a1(p1), a1(p2), a1(p3), a1(p4)} = {d11 (fc(p1))+ d 12(fc(p1)), d11(fc (p2))+ d 12(fc(p2)),d11 (fc(p3))+ d 12(fc(p3)), d11(fc(p4))+ d12(fc (p4))} = {d11(p1)+ d12(p1), d11(p2)+ d12(p2), d11(p3)+ d12(p3), d11(p4)+ d12(p4)}
Promotion 3: Submit an order on the site, get 1 reward point for each dollar spent. If you spend over $100, get 2 reward points for each dollar spent. If you spend over $200, get 3 reward points for each dollar spent.
Define the Promotion: Let
- Filters
- fc(L)=L (that is, fc does not eliminate any line items in L),
- Pattern filter
- fpc(P(L))=P(L), it does not eliminate any patterns
- Weighted range
- r1=[1,) with weight w=1 , R=(r1), that is, all the items are included in the pattern (an entire order);
- Pattern is defined as:
- P is configured by R, F, that is, (r1) and (fc)
- Distribution
- D =
and D is a tiered volume based spending distribution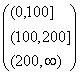
- Adjustment functions
- d1(L)= 1% of order total value custom numeric value (use the value as reward points),
d2(L)= 2% of order total value custom numeric value,
d3(L)= 3% of order total value custom numeric value - Rewards
- a1(L)=d 1(fc(L)),
a2(L)=d 2(fc(L)),
a3(L)=d 3(fc(L))With an order worth $250, a customer gets 750 reward points when this promotion is applied.
Conclusion
The activity of evaluating promotions consists of matching patterns in the current order and calculating the corresponding rewards.
The activity of creating promotions consists of configuring the various configurations (filter, pattern filter, weighted range, reward, adjustment, distribution) and assembling them together.
Related concepts